Disclaimer

This series is about current approaches to discriminative semi-supervised learning (SSL) for image classification with deep neural networks. We leave out a lot of the related work of SSL in combination with other approaches such as Support Vector Machines, Decision Trees, and other traditional approaches, as well as SSL approaches for text processing and natural language understanding. For a more detailed overview of SSL in general, check out other excellent reviews, e.g. by Olivier Chapelle et al. and Xiaojin Zhu

Introduction

Welcome to this blog post about semi-supervised learning (SSL) for deep neural networks. This is the first of a series of blog posts which will concentrate on the latest developments in the SSL literature for deep learning. More specifically, we will look into SSL approaches for image classification without the need for a generative model. Image classification is a popular task for deep neural networks such as convolutional neural networks (CNNs). Since it is fairly easy to evaluate and since we have many different, fully labelled data sets of varying size and complexity this task has garnered a lot of attention over the last couple of years. Currently, it is also one of the most common tasks to evaluate SSL approaches on. In the first part of this series, we will describe what SSL is, which types of SSL we will look at in this series, and why SSL is even useful. We will then look at some of the current approaches of SSL for image classification, namely graph based and entropy based SSL approaches. The next blog posts will continue on this theme and introduce more of the latest SSL approaches, such as consistency based SSL approaches and co-training.

What Is SSL?

When training an algorithm to learn something useful from any given data we can usually train them in a supervised or in an unsupervised manner. Supervised training assumes that we know the desired output for every data sample that we use during training. For example, in image classification that would mean that we know the class (cat, dog, bird, ...) for every image in our training set. Unsupervised training, on the other hand, means that we do know the class for none of our images in the training set. Semi-supervised learning (SSL) is a mixture of these two paradigms and assumes that we know the class for some of our images. Usually, in the SSL framework for image classification we have a large data set of images, but only know the correct class for a small subset of them. We could, of course, use the small subset of labelled data points to train a regular supervised model on them, however, the problem is that we will easily overfit the data, especially if we only have very few labelled samples and use a complex model such as a CNN. The idea of SSL is that we can get some information even from the unlabelled data points which can help us learn an overall better model, see Fig. 1 for an example.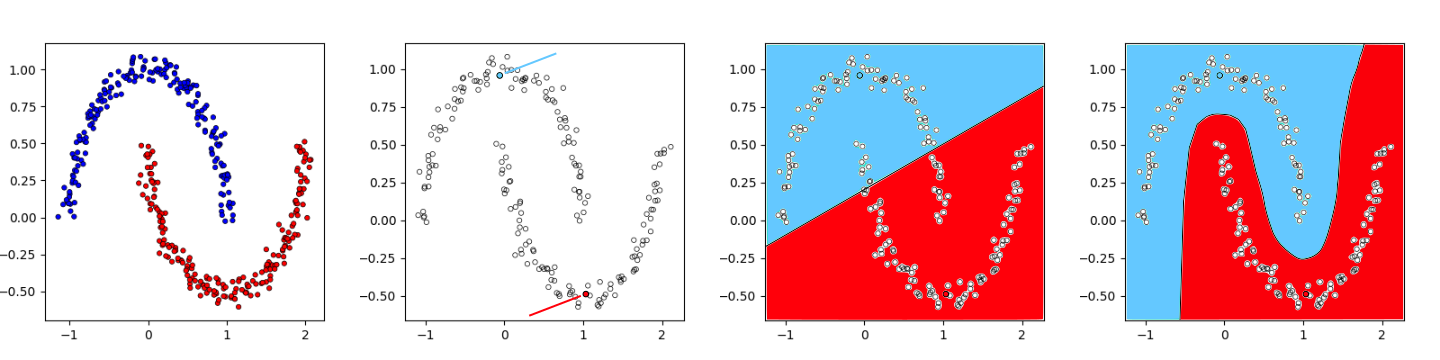

Let's assume we have a data set \(X_L=\{x_i\}_{i=1}^{l}\) consisting of \(l\) images and \(Y=\{y_i\}_{i=1}^{l}\) being the set of accompanying labels assigning each data point to one of \(C\) classes. Additionally, we have a number of images \(X_U=\{x_i\}_{i=l+1}^{n}\) for which we do not have accompanying labels. In SSL for image classification the full set of samples \(X\) consists of a set of labelled images \(X_L\) and unlabelled images \(X_U\): $$X = X_L ⋃ X_U,$$ where our set of labels \(Y\) only contains labels for the labelled subset \(X_L\). Our labels are usually encoded as one-hot vectors, meaning the label \(y_i \in \{0,1\}^C\) for the i-th data point in \(X_L\) belonging to class \(c\) is a vector of length \(C\) which is zero everywhere except at the class index: $$(y_i)_k = \begin{cases} 1 & \text{if}\ k = c, \\ 0 & \text{if}\ k \neq c \end{cases}.$$

We process our image input with some model \(f\) (often a CNN) which has learnable parameters \(θ\) and get as output a prediction of the class label \(\hat{Y}\): $$\hat{Y} = f_\theta(X).$$ In the case of neural networks, we usually use some form of gradient descent to optimize the model's parameters. Through this, the model parameters \(\theta\) are tweaked so that the model's output \(\hat{Y}\) gets closer to the ground truth labels \(Y\) for a given input \(X\). To use gradient descent we need a loss function \(L\) which we can use to optimize the model's parameters. In SSL the loss function usually contains (at least) two distinct parts: a supervised part \(L_{sup}\) and an unsupervised part \(L_{unsup}\). The supervised part of the loss function \(L_{sup}\) makes use of the labelled data samples to improve the model's quality. To use the unlabelled part of the data set, the unsupervised loss \(L_{unsup}\) imposes some sort of loss on the input that does not require ground truth labels. Most approaches for SSL differ mainly in how the unsupervised part of the loss function is calculated, while most models for image classification make use of the same supervised loss.

If the input is part of our labelled samples we know what the output of the model should be and we can compare the output of our model \(\hat{Y}\) with the known ground truth labels \(Y\). This is usually done by minimizing the cross-entropy between the model's output and the ground truth labels: $$L_{sup} = -\sum_{i} y_i\ log(\hat{y}_i) = H(y, \hat{y}).$$ Since this series of blog posts focuses on discriminative SSL approaches for image classification we will assume that the given loss function \(L\) is made up of two parts, none of which is dependent on a generative model: $$L = L_{sup} + \lambda L_{unsup},$$ where \(L_{sup}\) is the supervised loss calculated with labelled data points (usually the cross-entropy loss), \(L_{unsup}\) is the unsupervised loss which is either calculated for all data points or just the unlabelled ones, and \(\lambda\) is a factor that controls the influence of \(L_{unsup}\) on the total loss. How to calculate an informative loss on unlabelled data points is one of the main challenges of semi- and unsupervised learning and will be the focus of the rest of this post.

Which Types Of SSL Are There

There are several taxonomies that we can use to define different kinds of semi-supervised learning approaches. We will describe two such taxonomies, transductive vs inductive and generative vs discriminative, before looking at some of these approaches in more detail in the next section. Given some labelled and unlabelled samples (known in advance) transductive approaches have the goal to predict the labels for the unlabelled samples, i.e. to apply SSL techniques to label all provided unlabelled samples correctly. In other words, given a training set of labelled data points the goal is to predict the labels of only the given set of unlabelled data points, i.e. a learner is transductive if it only works on the labelled and unlabelled training data and cannot handle unseen data. Inductive models, on the other hand, try to lean a model to predict labels of previously unseen data. To learn this model the available labelled and unlabelled samples are used in one way or another. In this case, the prediction function is defined on the entire input space and inductive learner can, therefore, naturally handle previously unseen data at test time.

Another way to describe SSL techniques is in the setting of generative and discriminative models. Discriminative models try to predict the label \(y\) for a given input \(x\), i.e. they try to model \(P(y\vert x)\), which is usually done by some form of maximum likelihood estimation. Generative models, on the other hand, try to learn something about the data distribution \(P(x)\) itself, or, in the case of available labels, try to model the class-conditional density \(P(x\vert y)\) from which (for a known distribution of class labels) we can derive the joint distribution \(P(x,y) = P(x\vert y)\ P(y)\). As a consequence, generative models can be said to be more powerful than discriminative models. They also have no strict need for any labels, so can naturally be trained completely unsupervised and still learn useful characteristics about the data distribution. Generative models can be used for classification through the application of Bayes' rule: \(P(y\vert x) = \frac{P(x\vert y)\ P(y)}{P(x)}\), or through the definition of conditional probability: \(P(y\vert x) = \frac{P(x,y)}{P(x)}\). Nonetheless, discriminative models are (so far) much more popular for classification (i.e. discriminative) tasks, since they usually perform better on those tasks than generative models. A reason for this may be that the fitness measure for generative models is not discriminative so that better generative models are not necessarily better predictors of class labels. Additionally, density estimation generally is much more demanding than classification and Vapnik's principle for high-dimensional estimation states: When trying to solve some problem, one should not solve a more difficult problem as an intermediate step. Generative models try to estimate a density \(P(x)\) as an intermediate step, which is not strictly necessary for the final classification task. Discriminative models, on the other hand, directly estimate the labels \(P(y\vert x)\). This might be another reason for the current success and popularity for discriminative models for classification tasks. Nevertheless, generative models are widely used in the deep learning community and have led to remarkable success in the area of SSL. See for example Kingma et al. (2014) for one of the first approaches of combining generative models and deep neural networks for semi-supervised image classification. In spite of this, we will concentrate on discriminative approaches for semi-supervised image classification (which have also lead to state-of-the-art results) in the rest of this blog post.

For a more thorough background on SSL in general, details on generative models in the context of SSL, and information about SSL in the context of approaches like Support Vector Machines and Decision Trees check out the overviews by Olivier Chapelle et al. and Xiaojin Zhu. Additionally, see Oliver et al. for a current view on challenges of SSL approaches in academia and real-world scenarios. In the rest of this blog post, we will focus on inductive discriminative SSL approaches for image classification with deep neural networks.

Discriminative SSL Approaches For Image Classification

As mentioned above one of the main challenges is to find a way to train our models to make use of the unlabelled data points. In this post, we will focus on semi-supervised models that do not make use of generative models. Instead, we focus on approaches that adopt the training loss (often by combining a \(L_{unsup}\) with the supervised cross-entropy loss) in a way that makes it possible to use unlabelled data. This part is structured roughly by the different kinds of losses the different approaches use. We will first describe in more detail some graph and entropy based approaches. Graph based approaches work under the assumption that similar points in the data space (based on some predefined distance metric) should have the same label. Entropy based approaches encourage the model to make very confident predictions about all data points, regardless of whether labels are available or not. Future blog posts of this series will focus on other approaches, such as consistency based approaches or co-training.

Graph Based

Graph based approaches build a fully connected graph using the labelled and unlabelled data points. Nodes in the graph are the data points and connections between the nodes are usually undirected. The weight (strength) of the connection between two nodes (data points) is based on their similarity. For this, we need some kind of distance metric to calculate the distance/similarity between two data points. Given the graph, the assumption is then usually that points that have a strong connection (i.e. that are close to each other) are similar and, therefore, have the same label. Fig. 2 shows an example of the two-moons data set as a graph. In this example, we use the Euclidean distance as distance metric and the line width is proportional to the distance between the points. We can see that, for this simple data set, the vast majority of (strong) connections are between samples of the same class.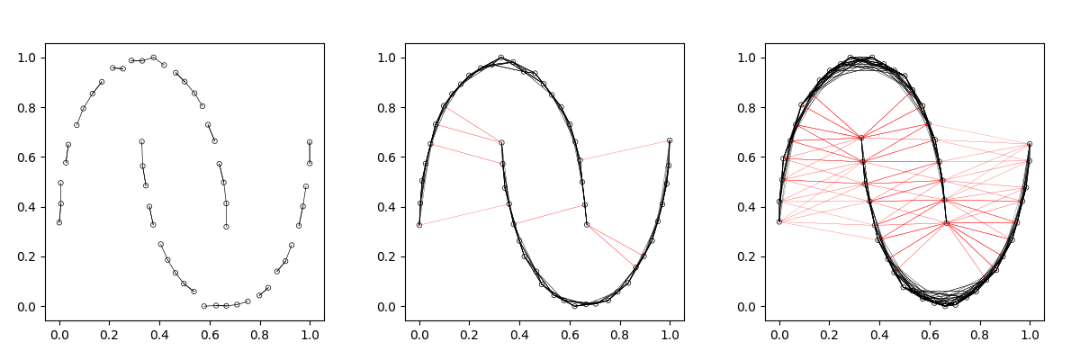

Most of the graph based approaches represent the connections by a similarity matrix \(W\) which is a \(n \times n\) matrix for our \(n\) data points, where the entry \(w_{ij}\) is a number that represents the strength of the connection between the two data samples \(w_i\) and \(w_j\). If we only have four data points and use the Euclidean distance as the distance measure, the initial similarity matrix \(W\) could look something like this: $$W = \begin{bmatrix}0 & 1.38 & 0.67 & 1.03\\ 1.38 & 0 & 1.02 & 0.67\\ 0.67 & 1.02 & 0 & 1.06\\ 1.03 & 0.67 & 1.06 & 0\\\end{bmatrix}$$ Often, the entries of \(W\) are row-normalized to obtain a probabilistic measurement of the similarities \(T\): \(w_{ij} = \frac{w_{ij}}{\sum_k^n w_{kj}}\). If we do this to the matrix from above we get as result: $$T = \begin{bmatrix}0 & 0.45 & 0.22 & 0.33\\ 0.45 & 0 & 0.33 & 0.22\\ 0.25 & 0.37 & 0 & 0.38\\ 0.37 & 0.25 & 0.38 & 0\\\end{bmatrix}$$

We can use this for approaches like label propagation, where we assign labels to unlabelled points based on the labels of their closest neighbours in the graph. One of the early works to use this approach is by Zhu et al. (2002) who perform label propagation to assign labels to their unlabelled data points. They construct the similarity matrix as we described above and have an additional matrix \(Y\) of shape \(n\times C\) (\(C\) is the number of classes) which contains the labels. For all labelled data points the corresponding row of \(Y\) contains its label (a one-hot vector), while the labels of unlabelled data are initialized with some values (e.g. all zeros). They then develop a label propagation algorithm in which the labels propagate through the graph based on the transition probabilities which are defined as in \(T\). The label propagation algorithm consists of three steps which are iteratively repeated until convergence:

1. Each node's label gets updated by multiplying the transition probability with all other nodes: \(Y = TY\).
2. \(Y\) is row-normalized to maintain the class probability interpretation
3. The labels for the labelled data points are clamped, i.e. reset to the ground truth value (a one-hot vector)

Weston et al. (2008) extend the label propagation algorithm to the deep learning setting. Again, it requires some predetermined distance metric to calculate the similarity between data points which is used to calculate the similarity matrix similarly to the previous approach before the optimization begins. In this work, the similarity matrix \(W\) is a sparse matrix where \(w_{ij}=1\) if \(x_i\) and \(x_j\) are neighbours and \(w_{ij}=0\) otherwise. There are different approaches of how to build such a similarity matrix based on the given distance metric, but one simple way is to use the \(k\)-nearest neighbours (kNN) approach for this. Based on our distance metric we assign the \(k\) closest data samples (in embedding space \(f_\theta(x_i)\)) as neighbours (\(w_{ij}\) = 1) and all other samples are not neighbours (\(w_{ij}\) = 0). As a result, if we start with the following similarity matrix as before: could look something like this: $$W = \begin{bmatrix}0 & 1.38 & 0.67 & 1.03\\ 1.38 & 0 & 1.02 & 0.67\\ 0.67 & 1.02 & 0 & 1.06\\ 1.03 & 0.67 & 1.06 & 0\\\end{bmatrix},$$ the resulting similarity matrix \(T\) for a 2-nearest neighbours (2NN) approach would be: $$T = \begin{bmatrix}1 & 1 & 0 & 1\\ 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1\\ 1 & 0 & 1 & 1\\\end{bmatrix}$$ \(T\) has ones on its diagonal since each point is also a neighbour of itself. For all labelled data points each point is a neighbour of all other points belonging to the same class. To calculate the unsupervised loss different losses are tested, which give varying results based on the network architecture. One of the most successful ones is the Siamese network loss applied directly to one of the network's embeddings, i.e. to the \(i\)'th layer. It is defined as: $$L_{unsup} = \begin{cases} \vert\vert f_\theta(x_i)-f_\theta(x_j)\vert\vert^2 & \text{if } w_{ij} = 1 \\ max(0, m-\vert\vert f_\theta(x_i)-f_\theta(x_j)\vert\vert )^2 & \text{if } w_{ij} = 0 \end{cases}$$ and encourages embeddings of neighbours to be close to each other, while embeddings of non-neighbours should have a distance of at least \(m\). The algorithm then first picks a random labelled sample and optimizes the supervised loss. Then, first a random pair of neighbours is picked and the unsupervised loss is optimized before a random pair of non-neighbours is picked and the unsupervised loss is optimized again. The key point here is that the unsupervised loss and the construction of the similarity matrix work directly on the embeddings from our model and not on the input data or labels as in previous approaches as e.g. label propagation. This approach is tested on the MNIST data set, achieving an overall best accuracy of 92.25% with 100 labelled data points and a CNN architecture.

Hoffer et al. (2016) take this one step further and optimizes the similarity distances directly. The goal is to optimize the data embeddings such that labelled samples of the same class form clusters and that embeddings of unlabelled samples are close to one of the clusters of the labelled embeddings. As in the previous approach, the distance is the Euclidean distance between the embeddings \(f_\theta(x_i)\). The similarity values for a given sample \(x_i\) are then calculated with respect to a set of labelled samples \((z_1, ..., z_C)\) and are represented as a discrete distribution for the probability of the sample \(x_i\) belonging to any of the given classes \(C\): $$P(x_i; z_1, ..., z_C)_k = \frac{e^{-\vert\vert f_\theta(x_i)-f_\theta(z_k)\vert\vert^2}}{\sum_j^C e^{-\vert\vert f_\theta(x_i)-f_\theta(z_j)\vert\vert^2}}, k\in\{1...C\}.$$ This assigns a probability \(P(x_i; z_1, ..., z_C)_k\) for sample \(x_i\) to be classified as belonging to class \(k\) under a 1-nearest neighbour classification rule when \(z_1, ..., z_C\) neighbours are given. The optimization takes place on this similarity distribution \(P(x_i; z_1, ..., z_C)\). For two labelled samples \(x_i, x_j\) belonging to the same class we want them to have a smaller distance in the embedding space than to any other sample \(x_k\) from a different class: $$\vert\vert f_\theta(x_i)-f_\theta(x_j)\vert\vert_2 < \vert\vert f_\theta(x_i)-f_\theta(x_k)\vert\vert_2.$$ Consequently, the first part of the loss (supervised) forces the model to build clusters in the embedding space (i.e. embeddings of the same class should be closer to each other than to embeddings of any other class) by minimizing the cross-entropy between the similarity distribution and the known, correct distribution. The correct distribution is the one-hot vector encoding the label and we can use this to minimize the cross-entropy between the one-hot vector and our similarity distribution \(P(x_i; z_1, ..., z_C)\): $$L_{sup} = H(\text{one-hot label}, P(x_i; z_1, ..., z_C))$$ The second part is the unsupervised loss and is there to reduce the overlap in clusters in the embedding space of unlabelled data by reducing the entropy of the similarity distribution. This means that the embedding of an unlabelled sample should be close to a given cluster of labelled samples, but far away from every other cluster. For a given unlabelled sample \(x_i\) there exists a labelled sample \(z_l\) which belongs to class \(l\in C\) such that $$\vert\vert f_\theta(x_i) - f_\theta(z_l)\vert\vert_2 \ll \vert\vert f_\theta(x_i) - f_\theta(z_k)\vert\vert_2,$$ for all other labelled samples \(z_k\) belonging to classes \(k\in C\setminus\{l\}\). The second part of the loss can be calculated on both labelled and unlabelled data points and is simply the entropy of the similarity distribution: $$L_{unsup} = H(P(x_i; z_1, ..., z_C)).$$ In practice, the algorithm randomly samples a set of labelled samples \(z_1, ..., z_{\vert C\vert}\) at each iteration and uses these samples to calculate the similarity distribution \(P\) for the rest of the data points in the current batch. The final model can then be used together with the kNN algorithm in the embedding space to classify new data points. This considerably improves the performance, e.g. achieving an overall best accuracy of 99.22% on the MNIST data set with 100 labelled samples and 79.7% on the CIFAR-10 data set with 4000 labelled samples.

Haeusser et al. (2017) introduce learning by association. The idea is to traverse from the embedding of a labelled sample to an embedding of an unlabelled sample and then back to a labelled sample's embedding. This "cycle" is counted as correct when both the start and the final embedding belong to images of the same class. While the method is not specifically formulated via graphs it bears many similarities and uses related approaches. The transition between embeddings, i.e. the decision which labelled or unlabelled embedding should be visited based on the current embedding is based on a transition probability which is obtained from a similarity measure between embeddings. The goal is to optimize the embeddings in a way that maximizes the probabilities of correct cycles, i.e. walks that start and finish within the same class. At train time labelled and unlabelled samples \(x_L\) and \(x_U\) are sampled and their embeddings \(z_L\) and \(z_U\) are obtained via a CNN. The similarity \(m_{ij}\) between two embeddings \(z_i\) and \(z_j\) is calculated as the dot product: \(m_{ij} = x_i\cdot x_j\). The transition probability \(w_{ij}\) between the two embeddings is then calculated by softmaxing the embeddings (similarly to the approach by Zhu et al.): $$w_{ij} = \frac{e^{m_{ij}}}{\sum_j e^{m_{ij}}}.$$ The round trip probability \(P^{ikj}\) of starting at embedding \(z_i\) and ending at embeddings \(z_j\) can then be calculated as: $$P^{ikj} = \sum_k w_{ik}w_{kj},$$ and the round trip probability of a correct walk is: $$P(\text{correct walk}) = \frac{1}{A}\sum_{i\sim j}P^{ikj},$$ where \(i\sim j \leftrightarrow \text{class}(z_i) = \text{class}(z_j)\) and \(A\) is the number of labelled samples in the batch. These probabilities are then used to construct two unsupervised losses. The first unsupervised loss, called the walker loss, penalizes incorrect walks and encourages a uniform probability for all walks back to the correct class. It optimizes the cross-entropy between the uniform probability of correct cycles T and the respective cycle probabilities: $$L_{unsup}^{walker} = H(T,P^{ikj}),$$ where \(T\) is the uniform target distribution which is \(\frac{1}{\vert c\vert}\) if class(\(z_i\))=class(\(z_j\)) and \(0\) otherwise and \(\vert c\vert\) is the number of occurrences of class \(c\in \{1,...,C\}\). However, there might be some unlabelled embeddings that represent difficult to classify data. The second unsupervised loss, called the visit loss, therefore minimizes the cross-entropy between the uniform target distribution \(V\) and the visit probabilities \(P^{visit}\). This encourages the model to use all unlabelled embeddings instead of only using "easy" embeddings for its cycles: $$L_{unsup}^{visit} = H(V, P^{visit}),$$ where \(P^{visit}_k = \langle P^{ik}\rangle_i\) are the probabilities of visiting unlabelled embedding \(z_k\) from some labelled embedding \(z_i\) and \(V = \langle\frac{1}{B}\rangle_k\) with \(B\) being the number of unlabelled samples in the batch. These two loss functions are then combined with the supervised loss in order to make use from both the labelled and unlabelled embeddings. This approach achieves an overall best accuracy of 99.11% on the MNIST data set with 100 labels and 94.86% on the SVHN data set with 1000 labelled samples.

Finally, Kamnitsas et al. (2018) try to increase the inter-class distance of the embeddings in order to make the graph more favourable for class separation. Their approach is similar to the one by Haeusser et al. we previously talked about with the main difference that Kamnitsas et al. allow longer walks in the embeddings space. While Haeusser et al. only had a short walk from labelled to unlabelled embedding and back, Kamnitsas et al. allow walks of arbitrary length and their walks are not restricted to alternate between labelled and unlabelled embeddings. At each training iteration labelled and unlabelled data points \(x_L\) and \(x_U\) are sampled and the model embeds them into feature space \(z=f_\theta(x)\). Then, a fully connected graph is built, where each embedding is connected to every other embedding. The weight of each connection is based on the similarity of the two embeddings: \(w_{ij} = e^{p(z_i,z_j)}\), where \(p\) is a similarity score, e.g. the Euclidean distance. Again, a transformation matrix is constructed as in Zhu et al. by normalizing \(w_{ij}\) to obtain a probability interpretation: \(w_{ij} = \frac{w_{ij}}{\sum_k w_{ik}}\). Then, label propagation (as in Zhu et al.) is performed to obtain the estimated class posteriors for the unlabelled data. One important note here is that the analytic solution for label propagation by Zhu et al. is differentiable, which is an important condition for the rest of the algorithm. However, instead of using these estimated labels for inference or to train the classifier, they are only used to capture the arrangement of clusters in the latent space in order to subsequently optimize this arrangement. The goal is to optimize this arrangement so that it forms one single cluster per class. To achieve this state, the transition probabilities \(w_{ij}\) between any two samples of a given class should be the same, while they should be zero for any inter-class transitions. This can be expressed by a (soft) constraint on the transition probabilities \(w_{ij}\): $$w_{ij} = \sum_c^C z_i^c\frac{z_j^c}{m^c},\ \ m^c = \sum_i z_i^c,$$ where \(z_i^c\) is the posterior probability for node \(i\) to belong to class \(c\) after label propagation, and \(m^c\) is the expected mass assigned to class \(c\). To encourage \(z\) to form clusters we can, therefore, minimize the cross-entropy between the ideal transition matrix (that adheres to the above constraint) and the current transition matrix. $$\hat{L}_{unsup} = \frac{1}{N^2}H(\hat{W},W),$$ where \(W\) is the transition matrix containing all current transition probabilities \(w_{ij}\) and \(\hat{W}\) is the ideal transition matrix. This loss is further adapted to include the intuition that existing clusters should not be disturbed during optimization. To do this the loss models a Markov chain of multiple transitions ("walks" in Haeusser et al.'s work) between data points in the graph. Transitioning between data points of the same class should have a high probability (since they are close by in the same cluster) while transitioning to points of another class should have a low probability. To calculate the probability \(m_{ij}\) that two nodes belong to the same class we can again use the class posterior estimations from the label propagation algorithm and calculate their dot product: \(m_{ij} = z_i\cdot z_j\) (as done by Haeusser et al.). The joint probability of transitioning from node \(i\) to node \(j\) can then be calculated as \(w_{ij}m_{ij}\). We can then calculate the probability of a Markov process to start at node \(i\), perform \((s-1)\) transitions between nodes of the same class and then end at any node \(j\) as the element \(W_{ij}^s\), with \(W_{ij}^s = (W\cdot M)^{s-1}W\), where \(\cdot\) denotes the elementwise product and \(M\) is the matrix containing all \(m_{ij}\).. The final unsupervised loss then optimizes \(W^s\) to be similar to the ideal transition probabilities \(\hat{W}\): $$L_{unsup} = \frac{1}{S}\sum_s^S\frac{1}{N^2} H(\hat{W}, W^s),$$ where \(S\) is the maximum number of Markov steps that are performed and the unsupervised loss is optimized jointly with the supervised loss (the cross-entropy loss on labelled samples). This approach achieves accuracies of 99.25% on the MNIST data set (100 labels), 94.31% on the SVHN data set (1000 labels), and 81.43% on the CIFAR-10 data set (4000 labels).

This concludes our section about graph based SSL approaches. They all have in common that they use a similarity measurement between data embeddings to optimize the embeddings. The intuition is that data points belonging to the same class should have similar embeddings (supervised loss) and that similar embeddings should belong to the same class and ideally be close to exactly one cluster of labelled data point embeddings (unsupervised loss). We now continue with entropy based approaches for SSL.

Entropy based

Entropy based models force models to be confident about their predictions. This is achieved by minimizing the model predictions' entropy. Since the predictions' entropy can be minimized without access to ground truth labels to compare against we can apply entropy minimization directly to the model's output for both labelled and unlabelled data. One of the first works based on this concept was done by Grandvalet et al. (2004). In this case, the unsupervised loss term is the entropy of predictions for the unlabelled data: $$L_{unsup} = \lambda\sum_i f_\theta (x_i) \text{ log}f_\theta(x_i),$$ for unlabelled input data \(x_i\), a model \(f\) with parameters \(\theta\), and \(\lambda\) weighting the influence of the unsupervised loss term.

Pseudo labelling, sometimes also called self-training or incremental training, is one of the most straight forward ways of doing SSL and can be seen as a special way to minimize the entropy of the model's predictions and was used by Rosenberg et al. (2005). In its simplest form, a classifier is trained on the labelled subset of data and then makes predictions on the unlabelled subset. Then, the subset of unlabelled data for which the classifier is very confident in its prediction (e.g. low entropy in its output) is added to the labelled data set, together with the labels predicted by the classifier. The classifier is then again trained on the (now larger) labelled data set and this process is repeated iteratively. This approach faces some problems though, such as adding wrong samples to the labelled data set which can hinder or even negatively affect the training process. Lee (2013) extended this approach to the deep learning approach and achieved an accuracy of 83.85% on the MNIST data set (100 labels). Since pseudo labelling encourages the model's predictions to be one-hot vectors in the long run (by adding predictions with high confidence as class labels to the supervised data set), this is effectively one of the early ways of entropy based SSL.

Sajjadi et al. (2016) took this approach to an extreme by adding an unsupervised loss term that forces the model's output to be close to a one-hot vector, i.e. 1 for the correct class and 0 for every other class. This is essentially a different way of enforcing a low entropy on the output, by adding a prior on the model output. Let \(f_j(x_i)\) be the \(j\)-th output unit of the model's prediction for \(x_i\) and \(C\) be the number of classes in our training set. To enforce the output to resemble a one-hot vector one can design a Boolean function with disjunction and conjunction which outputs "True" (1) if the output is of valid form (one-hot) and "False" (0) otherwise: $$\hat{L}_{unsup} = \lor_{j=1}^C (\land_{c=1, c\neq j}^C \lnot f_c\land f_j)$$ However, it is not straight forward to impose this prior in a loss function that has derivatives, which is necessary to optimize the model with a gradient descent algorithm. They get around this by approximating the loss function with a differentiable function. The conjunction of a set of binary variables \(\land_{i=1}^C\) is replaced by their product \(\prod_{i=1}^C x_i\), the not-operation \(\lnot x_i\) is replaced by \((1-x_i)\), and the disjunction of binary variables \(\lor_{i=1}^C x_i\) is replaced with their sum \(\sum_{i=1}^C x_i\). Through this they arrive at their final loss function which can be used with gradient descent: $$L_{unsup} = -\sum_{x_i}\left [\sum_{j=1}^C f_j(x_i)\prod_{c=1, c\neq j}^C (1-f_c(x_i))\right ].$$ This loss trains the model to predict only one class for a given input thereby minimizing its entropy. Using this approach they achieve an accuracy of 85.18% on the MNIST data set (80 labels), 84.7% on the SVHN data set (732 labels), and 72.29% on the CIFAR-10 data set (6000 labels).

Overall, we can see that entropy minimization methods on their own are not particularly successful when compared to e.g. graph based methods. While the approach is easy to implement the performance is much worse than other current approaches. This could be due to the fact that some confirmation bias is introduced and that current high capacity models might just overfit to the data. We can see this reflected in the fact that many approaches (especially for supervised classification) show that some entropy in the output prediction can be beneficial, especially at the beginning of the learning process. Intuitively, this can be described by the fact that some input classes might be more similar than others. For example, in the CIFAR-10 data set "cats" and "dogs" might be on average more similar than "cats" and "planes". As a result, a model that predicts an image to contain a "dog" and a "cat" with similar probability might be more desirable than a model that predicts an image to contain a "plane" and a "cat" with similar probability. This is especially the case at the beginning of the learning process, where it might be reasonable to first learn that "cats" and "dogs" have similar features (as opposed to "cats" and "planes"), before learning the finer differences later on. Techniques such as label smoothing and knowledge distillation make use of this intuition. In the same area, Pereyra et al. (2017) showed that penalizing outputs that are too confident can be a powerful regularizer for supervised learning. As we will see in the next blog posts, however, entropy based approaches are often combined with other SSL approaches, leading to overall state-of-the-art performance on multiple data sets in combination with other approaches.

Conclusion

In this blog post, we introduced the concept of discriminative semi-supervised learning for image classification. We have looked at some current approaches based on graphs and entropy minimization and, more specifically, how these approaches can be combined with current deep learning approaches to increase their performance even more. In the next blog posts, we will look more closely at other, highly successful, approaches of SSL in combination with deep learning, such as consistency regularization and co-training. If you have any questions or feedback don't hesitate to contact me. Otherwise, stay tuned for the next blog post.

Acknowledgements

We thank Manfred Eppe and Stefan Heinrich for their thoughtful feedback and support.